An AVL tree is a subtype of binary search tree. Named after it's inventors Adelson, Velskii and Landis, AVL trees have the property of dynamic self-balancing in addition to all the properties exhibited by binary search trees.
An Example Tree that is an AVL Tree
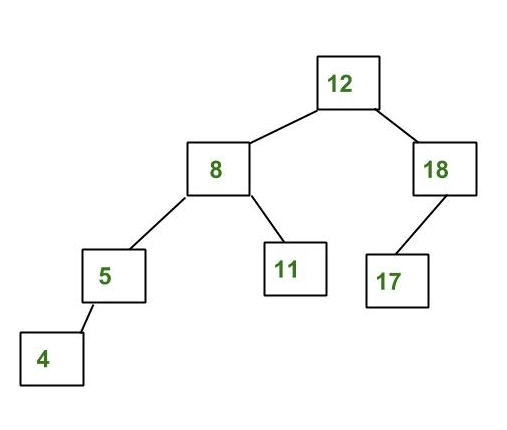
The above tree is AVL because differences between heights of left and right subtrees for every node is less than or equal to 1.
a. AVL Tree Operations: Insertion
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing. Following are two basic operations that can be performed to re-balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
1) Left Rotation
2) Right Rotation
T1, T2 and T3 are subtrees of the tree
rooted with y (on the left side) or x (on
the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the
following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertionLet the newly inserted node be w
1) Perform standard BST insert for w.
2) Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
3) Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that needs to be handled as x, y and z can be arranged in 4 ways. Following are the possible 4 arrangements:
a) y is left child of z and x is left child of y (Left Left Case)
b) y is left child of z and x is right child of y (Left Right Case)
c) y is right child of z and x is right child of y (Right Right Case)
d) y is right child of z and x is left child of y (Right Left Case)
a) Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
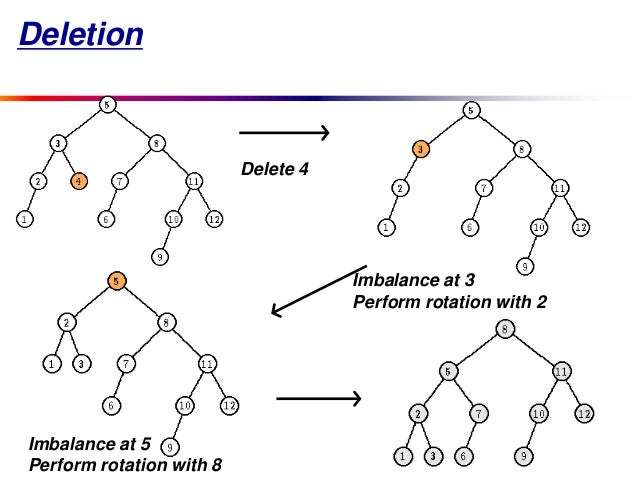
b. AVL Tree Operations: deletion
•Delete the node as in ordinary
Binary Search Tree.
•The deleted node will be a leaf or
a node with one child.
•Trace the path from the (parent of)
deleted leaf towards the root. For each node P encountered, check if height of
left(P) and right(P) differ by at most 1.
•If Yes, proceed to parent(P).
•If No, fix sub tree P either by
single rotation or double rotation (as in insertion).
•After we perform rotation at P, we
may have to perform a rotation at some ancestor of P. Thus, we
must continue to trace the path until we reach the root.
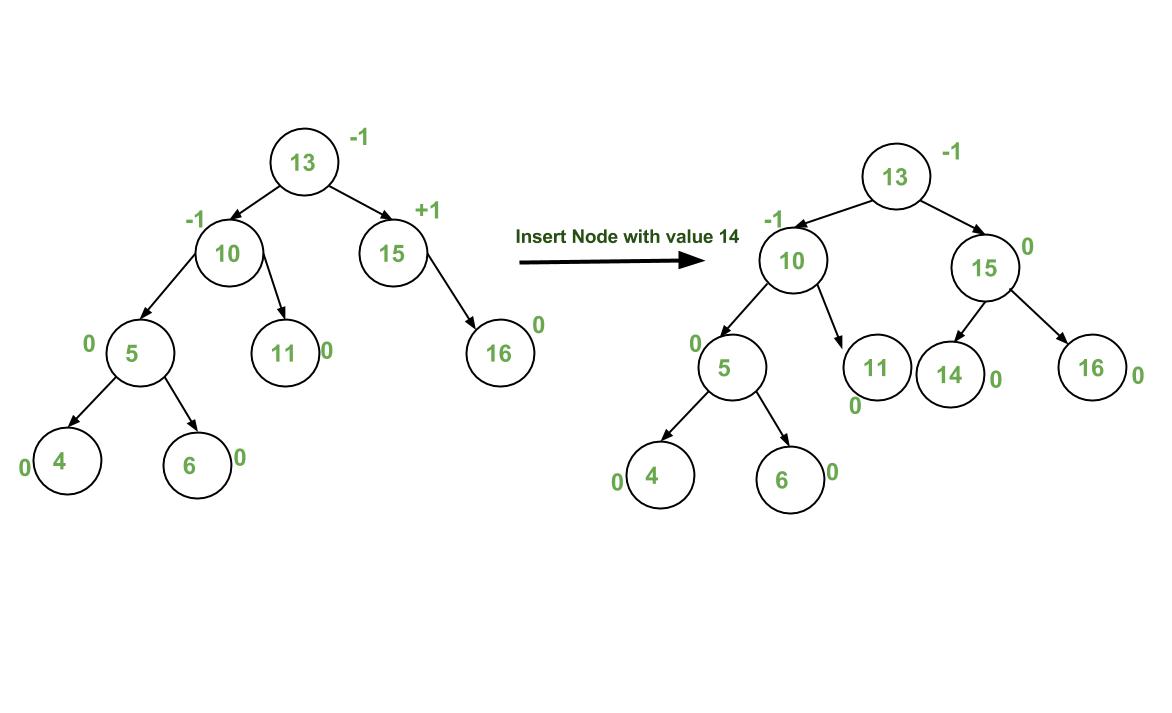
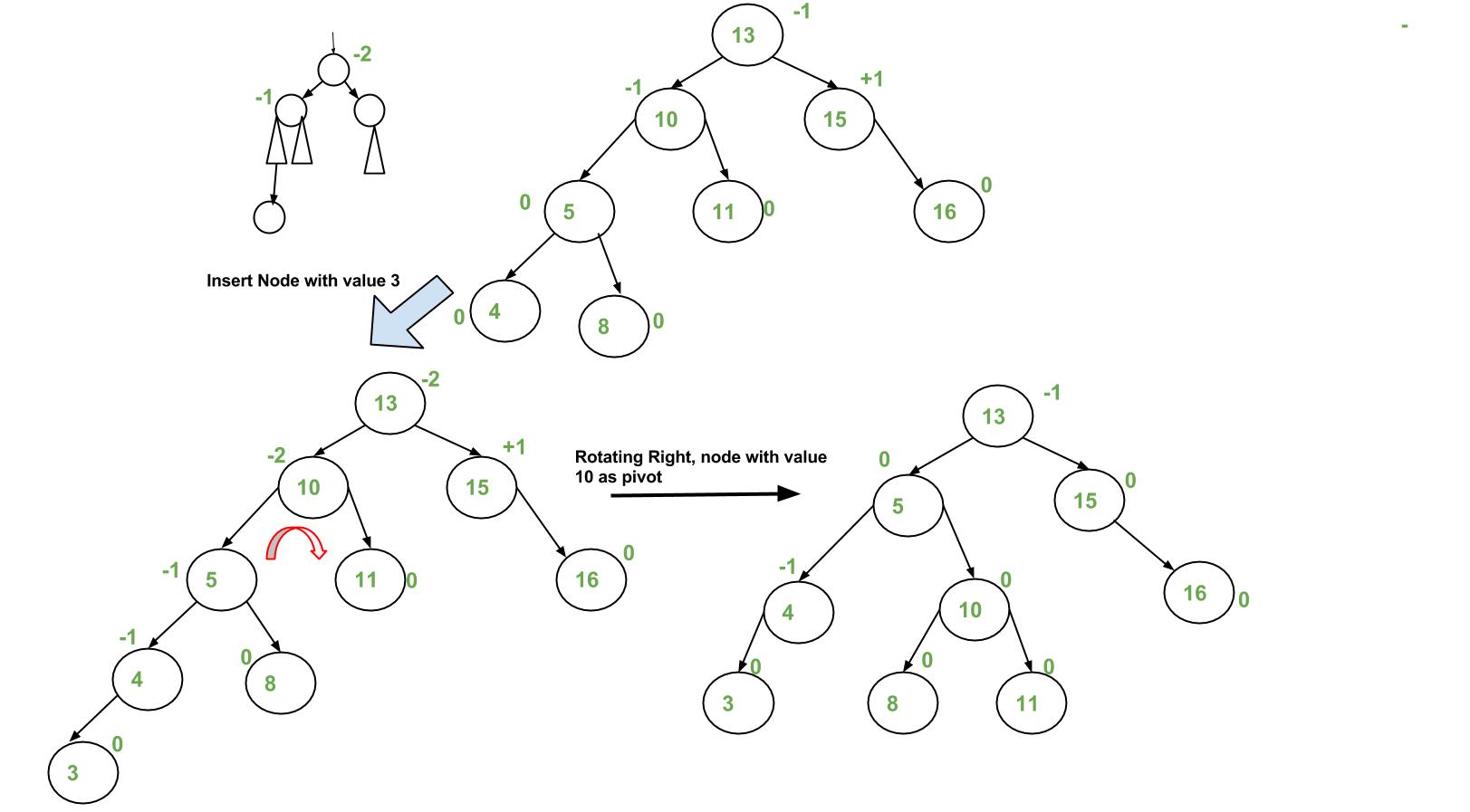
Example AVL and B-trees:
Insert: 5, 6, 7, 0, 4, 3, 8
Delete: 3, 4, 8
Insert: 5, 6, 7, 0, 4, 3, 8
Delete: 3, 4, 8
AVL Tree:
insertion:
after deletion:
B-Tree:
insertion:
after deletion:



No comments:
Post a Comment